Ransac 算法
前言:
最近在做相机-激光雷达(MID70)联合标定的时候,采用港大火星实验室的一个自动标定工作,为了优化表现,于是开始研究里面的参数。
我注意到一个参数名称是 Ransac,ransac.min_dis
RANSAC 算法,又称 Random Sample Concensus,是为了寻找一组采样点的 outlier 的随机迭代算法。
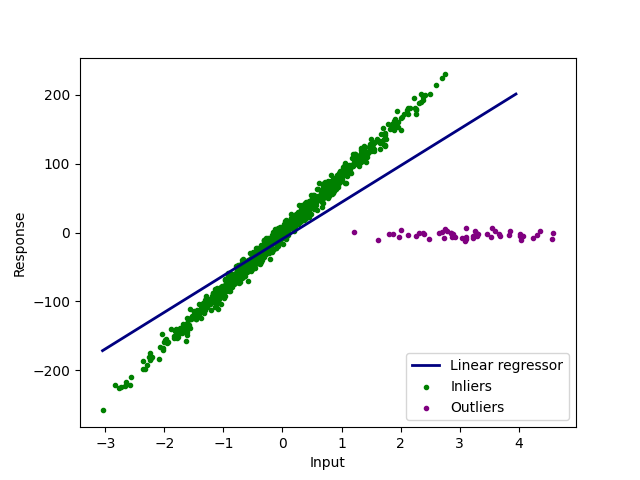
RANSAC 的随机性,说明它是一个 non-deterministic 算法,它相对于最小二乘拟合法的优势在于:RANSAC 考虑了 inlier 和 outlier 对模型的影响。最小二乘法将所有数据点都考虑到模型当中,对于下面的示例,最小二乘法会被噪点带偏,然而 RANSAC 能够区分数据点中 inlier 和 outlier 这两个不同的部分,从而能够成功应对这种情况。
算法流程
RANSAC 算法的流程也很容易理解,具体如下:
从全部数据点中选取一部分,我们将假设它包含于 inlier 点集
对选取的点集进行模型拟合(这里的模型可以根据自己的需要选取,比如线性回归)
根据一个阈值,寻找与模型估计在误差范围内的所有点
判断上一步找到的点的个数是否大于阈值,如果是,则计算 fitness,并更新最优解
回到 1 进行新的一轮迭代
这个算法在雷达相机匹配中的作用是,分割出一个体素中存在的平面。为什么可以实现这个功能?
只要把点集的维度拓宽为 3 维,模型从二维线性回归变到三维线性回归。
最坏情况分析
事实上,我们可以证明模型的迭代次数越多,1 就越有可能获得全部位于 inlier 中的点,从而获得较优的模型估计。证明:
记 \(\omega = \frac{\text{inliers num}}{\text{total sample points num}}\),设 \(p\) 为经过 \(k\) 轮迭代,每轮采样点有 \(n\) 个的情况下,至少有一次获得全部位于 inlier 中点的概率。
\[ \begin{aligned} 1-p &= (1-\omega^n)^k \\ k &= \frac{\log (1-p)}{\log (1-\omega^n)} \end{aligned} \]
不过,上面的计算假设了每次抽样是独立的(可以放回)
参数的整定
根据算法流程,我们发现主要有两个关键参数
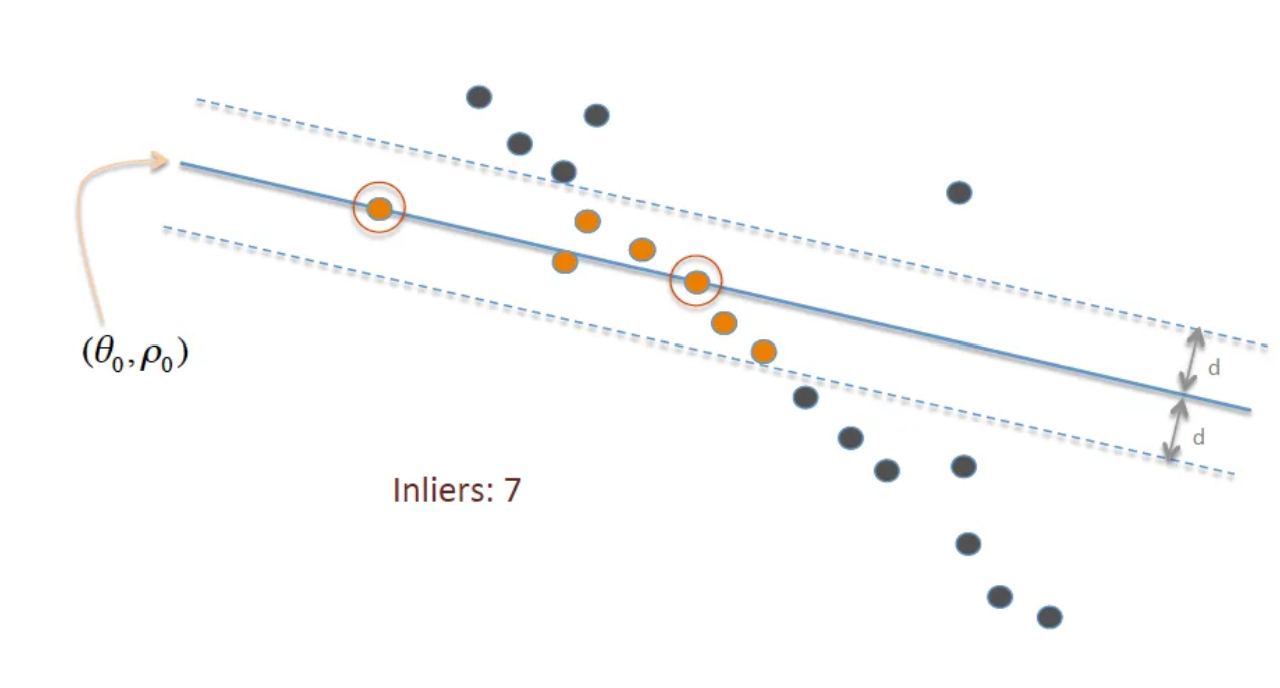
Ransac.dis_threshold 可以通过下图直观理解
其中 \(d\) 代表误差,这会影响算法流程中第 3 步。这个参数的整定取决于 inlier 的方差。
Ransac.iter_num 需要根据上一小节进行合理分析
注意到 \(\omega\) 越小的情况下,我们应该迭代更多次,才能让结果收敛。